Regularization in statistical models

Author

Jong-Hoon Kim

Published

February 2, 2025

Code 
library(tidyverse)
library(glmnet)
library(caret)
library(recipes)
set.seed(123)

Introduction

Regularization is a fundamental technique in statistical modeling that helps prevent overfitting and improves model generalization. This blog post explores different regularization methods, their implementation in R, and their practical applications, with a special focus on scenarios where the number of parameters exceeds the number of observations (p > n).

Understanding Regularization

Regularization works by adding a penalty term to the model’s loss function, effectively constraining the magnitude of model coefficients. The three most common types are:

  1. Ridge (L2)
  2. Lasso (L1)
  3. Elastic Net (combination of L1 and L2)

Simulation Study: When p > n

Let’s first create a scenario where we have more parameters than observations:

Code 
# Generate synthetic data
n <- 50  # number of observations
p <- 100 # number of predictors

# Create sparse true coefficients (most are zero)
true_beta <- rep(0, p)
true_beta[1:5] <- c(1.5, -0.8, 1.2, -0.5, 0.9)

# Generate predictor matrix
X <- matrix(rnorm(n * p), nrow = n)
# Generate response with some noise
y <- X %*% true_beta + rnorm(n, sd = 0.5)

# Convert to data frame
data <- as.data.frame(X)
data$y <- y

Ridge Regression (L2)

Ridge regression adds the sum of squared coefficients to the loss function:

Code 
# Prepare data for glmnet
x_matrix <- as.matrix(data[, -ncol(data)])
y_vector <- data$y

# Fit ridge regression
ridge_fit <- glmnet(x_matrix, y_vector, alpha = 0, 
                    lambda = exp(seq(-3, 5, length.out = 100)))

# Cross-validation to find optimal lambda
cv_ridge <- cv.glmnet(x_matrix, y_vector, alpha = 0)

# Plot cross-validation results
plot(cv_ridge)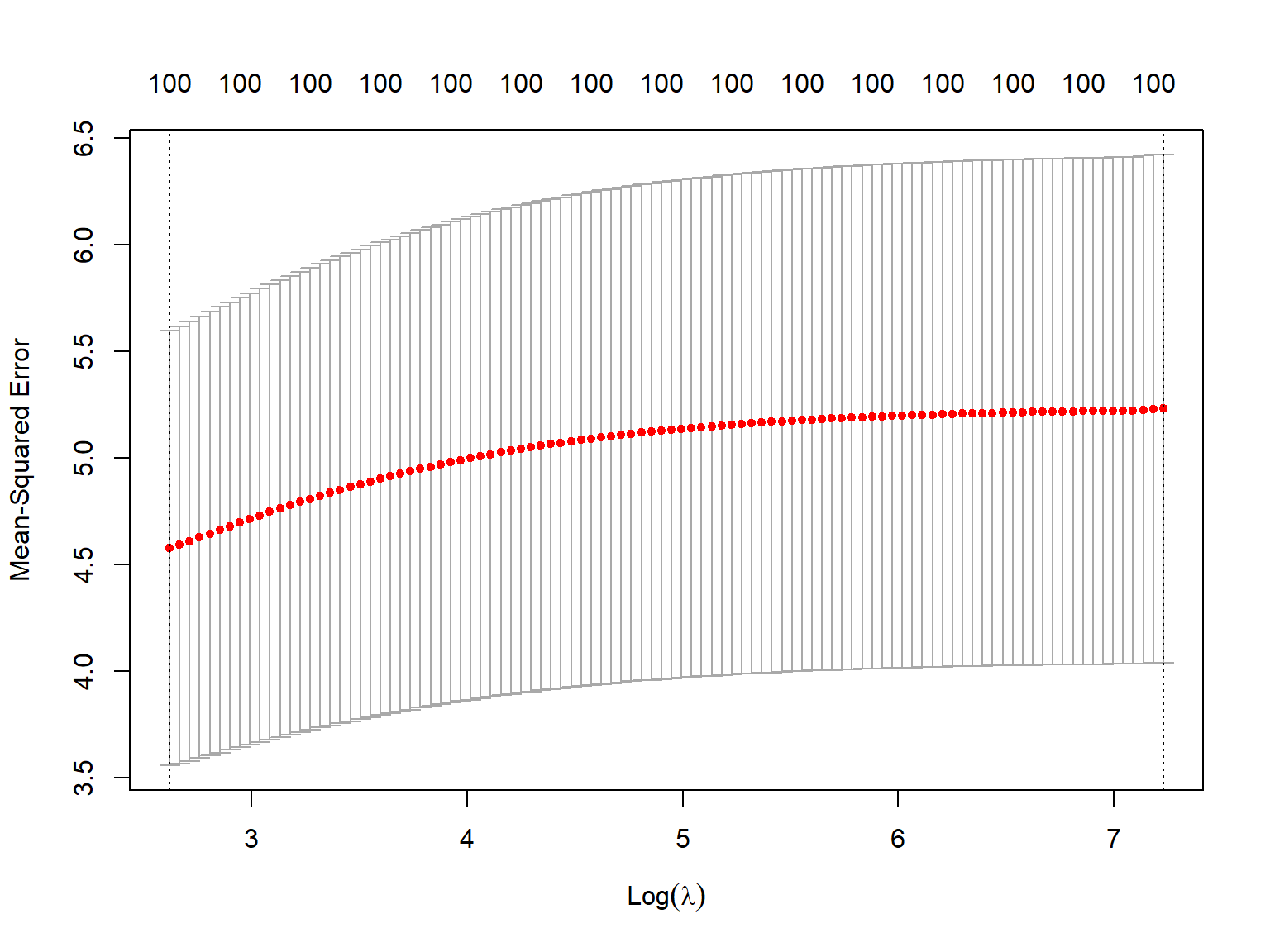

Lasso Regression (L1)

Lasso regression uses absolute value penalties and can perform variable selection:

Code 
# Fit lasso regression
lasso_fit <- glmnet(x_matrix, y_vector, alpha = 1,
                    lambda = exp(seq(-3, 5, length.out = 100)))

# Cross-validation
cv_lasso <- cv.glmnet(x_matrix, y_vector, alpha = 1)

# Plot solution path
plot(lasso_fit, xvar = "lambda", label = TRUE)

Elastic Net

Elastic Net combines both L1 and L2 penalties:

Code 
# Fit elastic net with alpha = 0.5
enet_fit <- glmnet(x_matrix, y_vector, alpha = 0.5,
                   lambda = exp(seq(-3, 5, length.out = 100)))

# Cross-validation
cv_enet <- cv.glmnet(x_matrix, y_vector, alpha = 0.5)

# Compare coefficients at optimal lambda
coef_comparison <- data.frame(
  true = true_beta,
  ridge = as.vector(coef(cv_ridge, s = "lambda.min"))[-1],
  lasso = as.vector(coef(cv_lasso, s = "lambda.min"))[-1],
  elastic = as.vector(coef(cv_enet, s = "lambda.min"))[-1]
)

# Plot first 20 coefficients
head(coef_comparison, 20)
   true        ridge      lasso       elastic
1   1.5  0.168206623  1.4215046  1.3290087822
2  -0.8 -0.136466379 -0.7070713 -0.7202401708
3   1.2  0.159580168  1.1339067  1.0787191944
4  -0.5 -0.036699418 -0.2745075 -0.2490259735
5   0.9  0.074879809  0.8026272  0.7517043315
6   0.0 -0.023896821  0.0000000  0.0000000000
7   0.0 -0.009236366  0.0000000  0.0000000000
8   0.0 -0.015842275  0.0000000  0.0000000000
9   0.0 -0.104338887  0.0000000 -0.0146134033
10  0.0 -0.011447505  0.0000000  0.0000000000
11  0.0  0.044632265  0.0000000  0.0000000000
12  0.0  0.005038114  0.0000000  0.0000000000
13  0.0 -0.008216405  0.0000000  0.0000000000
14  0.0  0.028400026  0.0000000  0.0001638061
15  0.0  0.011236623  0.0000000  0.0000000000
16  0.0  0.003305804  0.0000000  0.0000000000
17  0.0  0.017521241  0.0000000  0.0000000000
18  0.0  0.021065650  0.0000000  0.0000000000
19  0.0 -0.005236160  0.0000000  0.0000000000
20  0.0  0.039430620  0.0000000  0.0000000000

Regularization in p > n Scenarios

When the number of parameters (p) exceeds the number of observations (n), regularization becomes not just useful but essential. Here’s why:

  1. Mathematical Necessity: Without regularization, the problem is ill-posed as there are infinitely many solutions that perfectly fit the training data.

  2. Variance Reduction: Regularization helps reduce the variance of parameter estimates, which is particularly important when we have limited data.

  3. Feature Selection: Lasso and Elastic Net can help identify the most important features, which is crucial when dealing with high-dimensional data.

Let’s demonstrate this with a comparison of prediction errors:

Code 
# Generate test data
X_test <- matrix(rnorm(n * p), nrow = n)
y_test <- X_test %*% true_beta + rnorm(n, sd = 0.5)

# Calculate MSE for each method
mse <- data.frame(
  Method = c("Ridge", "Lasso", "Elastic Net"),
  MSE = c(
    mean((predict(cv_ridge, newx = X_test) - y_test)^2),
    mean((predict(cv_lasso, newx = X_test) - y_test)^2),
    mean((predict(cv_enet, newx = X_test) - y_test)^2)
  )
)

print(mse)
       Method       MSE
1       Ridge 6.3827969
2       Lasso 0.4183443
3 Elastic Net 0.5025287

Best Practices and Recommendations

When working with p > n scenarios:

  1. Start with Cross-Validation: Always use cross-validation to select the optimal regularization parameter (λ).

  2. Consider Multiple Methods: Try different regularization approaches as their performance can vary depending on the underlying data structure.

  3. Scale Features: Standardize predictors before applying regularization to ensure fair penalization.

  4. Monitor Sparsity: If interpretability is important, prefer Lasso or Elastic Net as they can produce sparse solutions.

Conclusion

Regularization is particularly crucial in p > n scenarios, where it helps: - Prevent perfect but meaningless fits to training data - Reduce model complexity - Identify important features - Improve prediction accuracy on new data

The choice between Ridge, Lasso, and Elastic Net depends on your specific needs regarding sparsity, prediction accuracy, and interpretability.

References

  1. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning.
  2. Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net.
  3. James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning.