모델과 현실: 수학으로 감염병 확산을 읽다

수학 모델로 감염병 확산을 예측한다. 현실과 얼마나 맞을까? 코로나19는 이 질문의 정답을 알려줬다.

모델은 단순화된 현실이다

감염병 수학 모델은 현실의 복사본이 아니다. 그저 도구일 뿐이다.

지하철 노선도를 생각해보자. 실제 지리를 정확히 반영하진 않는다. 하지만 길 찾기엔 충분하다. 감염병 모델도 마찬가지다. 복잡한 현실을 단순화해 핵심만 보여준다.

가장 기본적인 감염병 모델은 SIR 모델이다. S는 감염 가능한 사람(Susceptible), I는 감염된 사람(Infected), R은 회복된 사람(Recovered)을 뜻한다. 이 세 집단이 시간에 따라 어떻게 변화하는지 보여준다.

시간이 지날수록 S는 줄고, I는 늘었다가 줄고, R은 계속 늘어난다. 단순하다. 그러나 감염병 확산의 기본 패턴을 정확히 보여준다.

Code

library(deSolve)
library(ggplot2)
library(tidyr)
library(hrbrthemes)

# SIR 모델 정의
sir_model <- function(time, state, parameters) {
  with(as.list(c(state, parameters)), {
    dS <- -beta * S * I
    dI <- beta * S * I - gamma * I
    dR <- gamma * I
    return(list(c(dS, dI, dR)))
  })
}

# 매개변수 설정
parameters <- c(beta = 0.3, gamma = 0.1)
initial_state <- c(S = 0.99, I = 0.01, R = 0.0)
times <- seq(0, 100, by = 1)

# 모델 실행
output <- as.data.frame(ode(y = initial_state, times = times, 
                          func = sir_model, parms = parameters))

# 데이터 형식 변환
output_long <- pivot_longer(output, cols = c("S", "I", "R"), 
                           names_to = "상태", values_to = "비율")

# 표시할 레이블 설정
output_long$상태 <- factor(output_long$상태, 
                         levels = c("S", "I", "R"),
                         labels = c("감염 가능", "감염됨", "회복됨"))

# 그래프 그리기
ggplot(output_long, aes(x = time, y = 비율, color = 상태)) +
  geom_line(size = 1.2) +
  labs(title = "전형적인 감염병 확산 패턴",
       subtitle = "SIR 모델에 기반한 시뮬레이션",
       x = "시간 (일)", 
       y = "인구 비율",
       caption = expression(paste("기본 재생산 지수(", R[0], ") = 3.0"))) +
  scale_color_manual(values = c("감염 가능" = "#3498db", 
                               "감염됨" = "#e74c3c", 
                               "회복됨" = "#2ecc71")) +
  theme_ipsum_rc() +
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        plot.title = element_text(face = "bold", size = 16),
        plot.subtitle = element_text(size = 12),
        axis.title = element_text(size = 12))

기본 SIR 모델: 시간에 따른 감염 가능(S), 감염됨(I), 회복됨(R) 인구의 변화

Code

  # annotate("text", x = 22, y = 0.25, label = "최대 감염자 수", 
  #          color = "#e74c3c", fontface = "bold") +
  # annotate("segment", x = 22, y = 0.23, xend = 18, yend = 0.19,
  #          arrow = arrow(length = unit(0.3, "cm")), color = "#e74c3c")

직접 실험할 수 없을 때, 모델이 답한다

“학교를 2주 닫으면 코로나 확산이 얼마나 줄어들까?”

이런 질문에 답하려면 어떻게 해야 할까? 실제로 학교를 닫았다 열었다 실험할 수는 없다. 위험하다. 비용도 많이 든다.

모델은 이런 가상 실험을 가능하게 한다. 컴퓨터 속에서 다양한 상황을 시뮬레이션 할 수 있다. 철학자들은 이를 “대리 추론”(surrogate reasoning)이라고 부른다. 현실 대신 모델로 추론하는 것이다.

Code

library(deSolve)
library(ggplot2)
library(dplyr)

# 감염병 모델 (거리두기 효과 포함)
intervention_model <- function(time, state, parameters) {
  with(as.list(c(state, parameters)), {
    beta_t <- beta * intervention_effect(time, int_start, int_duration, int_strength)
    dS <- -beta_t * S * I
    dI <- beta_t * S * I - gamma * I
    dR <- gamma * I
    return(list(c(dS, dI, dR)))
  })
}

# 개입 효과 함수
intervention_effect <- function(time, start, duration, strength) {
  if (time >= start && time < start + duration) {
    return(1 - strength)  # 개입 기간 중 효과
  } else {
    return(1)  # 개입 없음
  }
}

# 시나리오 생성 함수
generate_scenario <- function(int_strength, label) {
  parameters <- c(beta = 0.3, gamma = 0.1, 
                 int_start = 20, int_duration = 30, 
                 int_strength = int_strength)
  
  initial_state <- c(S = 0.99, I = 0.01, R = 0.0)
  times <- seq(0, 100, by = 1)
  
  output <- as.data.frame(ode(y = initial_state, times = times, 
                            func = intervention_model, parms = parameters))
  output$scenario <- label
  return(output)
}

# 시나리오 실행
no_intervention <- generate_scenario(0, "조치 없음")
mild_intervention <- generate_scenario(0.3, "약한 거리두기")
moderate_intervention <- generate_scenario(0.6, "중간 거리두기")
strong_intervention <- generate_scenario(0.8, "강한 거리두기")

# 데이터 결합
all_scenarios <- bind_rows(no_intervention, mild_intervention,
                          moderate_intervention, strong_intervention)

# 그래프 그리기
ggplot(all_scenarios, aes(x = time, y = I, color = scenario, linetype = scenario)) +
  geom_line(size = 1.2) +
  labs(title = "사회적 거리두기 강도에 따른 감염 곡선 변화",
       subtitle = "거리두기 개입은 20일차에 시작하여 30일간 지속",
       x = "시간 (일)", 
       y = "감염자 비율",
       caption = expression(paste("기본 재생산 지수(", R[0], ") = 3.0"))) +
  scale_color_manual(values = c("조치 없음" = "#e74c3c", 
                               "약한 거리두기" = "#f39c12", 
                               "중간 거리두기" = "#3498db", 
                               "강한 거리두기" = "#2ecc71")) +
  scale_linetype_manual(values = c("조치 없음" = "solid", 
                                  "약한 거리두기" = "dashed", 
                                  "중간 거리두기" = "dotdash", 
                                  "강한 거리두기" = "longdash")) +
  theme_ipsum_rc() +
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        plot.title = element_text(face = "bold", size = 16),
        plot.subtitle = element_text(size = 12),
        axis.title = element_text(size = 12)) +
  annotate("rect", xmin = 20, xmax = 50, ymin = -Inf, ymax = Inf,
           alpha = 0.1, fill = "gray50") +
  annotate("text", x = 35, y = 0.01, label = "개입 기간", 
           fontface = "italic", color = "gray50")

코로나19 개입 효과 비교: 다른 강도의 사회적 거리두기가 감염 곡선에 미치는 영향

코로나19는 모델의 강점과 한계를 동시에 보여줬다

코로나19 초기, 모델은 중요한 역할을 했다. 병원에 수용될 환자수를 예측하고, 사회적 거리두기(social distancing)의 효과를 추정했다. 정책 결정에 도움을 줬다.

그러나 예측이 빗나간 경우도 많았다. 이유는 여러 가지다. 바이러스에 대한 정보가 부족했다. 사람들의 행동 변화를 예측하기 어려웠다. 새로운 변이가 등장했다.

영국 임페리얼 칼리지(Imperial College)의 모델은 초기에 큰 주목을 받았다. 아무런 조치를 취하지 않으면 영국에서만 51만 명이 사망할 수 있다고 예측했다. 실제로는 그보다 훨씬 적은 사람이 사망했다. 정부의 개입과 사람들의 행동 변화 때문이었다.

모델은 틀렸지만, 정책 결정에 영향을 미쳤다. 유용했다.

Code

library(ggplot2)
library(lubridate)
library(dplyr)

# 가상 데이터 생성 (실제 데이터를 시뮬레이션)
set.seed(123)

# 날짜 생성
dates <- seq(as.Date("2020-03-01"), as.Date("2020-06-30"), by = "day")

# 초기 예측 모델 (과대 예측)
initial_model <- 100 * exp(0.14 * 1:length(dates))
initial_model[initial_model > 10000] <- 10000 + (initial_model[initial_model > 10000] - 10000) * 0.1
initial_model <- pmin(initial_model, 15000)

# 업데이트된 모델 (더 정확함)
updated_model <- 50 * exp(0.12 * 1:length(dates))
updated_model <- pmin(updated_model, 5000)

# 실제 사례 (락다운 효과 반영)
actual_cases <- 50 * exp(0.12 * 1:40)
lockdown_effect <- exp(-0.03 * 1:(length(dates) - 40))
actual_cases <- c(actual_cases, actual_cases[40] * lockdown_effect)
actual_cases <- actual_cases + rnorm(length(dates), 0, actual_cases * 0.05)
actual_cases <- pmax(0, actual_cases)

# 데이터프레임 만들기
model_data <- data.frame(
  date = rep(dates, 3),
  cases = c(initial_model, updated_model, actual_cases),
  type = factor(rep(c("초기 모델 (3월 1일)", "업데이트된 모델 (4월 1일)", "실제 사례"), each = length(dates)))
)

# 락다운 시작일
lockdown_date <- as.Date("2020-04-10")

# 그래프 그리기
ggplot(model_data, aes(x = date, y = cases, color = type, linetype = type)) +
  geom_line(size = 1.2) +
  labs(title = "코로나19 모델 예측과 실제 확진자 수 비교",
       subtitle = "초기 모델은 과대 예측, 업데이트된 모델은 더 정확함",
       x = "날짜", y = "일일 확진자 수", caption = "가상 데이터 기반 시뮬레이션") +
  scale_color_manual(values = c("초기 모델 (3월 1일)" = "#e74c3c", 
                              "업데이트된 모델 (4월 1일)" = "#3498db", 
                              "실제 사례" = "#2ecc71")) +
  scale_linetype_manual(values = c("초기 모델 (3월 1일)" = "dashed", 
                                 "업데이트된 모델 (4월 1일)" = "dotdash", 
                                 "실제 사례" = "solid")) +
  theme_ipsum_rc() +
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        plot.title = element_text(face = "bold", size = 16),
        plot.subtitle = element_text(size = 12),
        axis.title = element_text(size = 12)) +
  geom_vline(xintercept = lockdown_date, linetype = "dashed", color = "gray50") +
  annotate("text", x = lockdown_date - days(1), y = 15000, 
           label = "락다운 시작", color = "gray50", fontface = "italic", hjust=1)

모델 예측과 실제 데이터 비교: 코로나19 첫 물결(가상 데이터)

더 나은 모델을 위한 다섯 가지 방법

모델을 현실에 더 가깝게 만들려면 어떻게 해야 할까?

1. 실증적 검증(empirical validation): 모델 결과를 실제 데이터와 지속적으로 비교한다.
2. 민감도 분석(sensitivity analysis): 매개변수(parameter) 변화가 결과에 어떤 영향을 미치는지 이해한다.
3. 앙상블 모델링(ensemble modeling): 여러 모델을 함께 사용해 더 균형 잡힌 전망을 얻는다.
4. 이질성 반영(incorporating heterogeneity): 연령, 지역, 행동 패턴 등 다양한 요소를 모델에 추가한다.
5. 학제 간 협력(interdisciplinary collaboration): 역학자(epidemiologist), 의사, 행동 과학자, 데이터 과학자가 함께 모델을 개발한다.

현재 많은 연구팀이 이러한 방향으로 모델을 개선하고 있다. 하버드 대학의 연구팀은 모바일 데이터를 활용해 사람들의 이동 패턴을 모델에 반영했다. 더 정확한 예측이 가능해졌다.

Code

library(ggplot2)
library(dplyr)
library(ggrepel)

# 모델 유형별 데이터
model_types <- data.frame(
  complexity = c(1, 2, 3, 5, 6, 8),
  accuracy = c(0.4, 0.55, 0.7, 0.8, 0.83, 0.85),
  type = c("SIR", "SEIR", "SEIR+", "연령 구조화 모델", "공간적 모델", "행동 적응형 모델"),
  features = c("기본 감염-회복 역학", 
              "잠복기 추가", 
              "무증상 감염자 추가", 
              "연령별 취약성과 접촉 패턴", 
              "지역 간 이동과 공간적 이질성", 
              "행동 변화와 정책 대응의 피드백 루프")
)

# 과적합 곡선 데이터
x_curve <- seq(0.5, 10, length.out = 100)
accuracy_curve <- 0.9 * (1 - exp(-0.5 * x_curve))
overfitting_curve <- 0.9 * (1 - exp(-0.5 * x_curve)) - (0.3 * pmax(0, x_curve - 5)^2 / 30)

curve_data <- data.frame(
  complexity = c(x_curve, x_curve),
  accuracy = c(accuracy_curve, overfitting_curve),
  dataset = rep(c("이론적 정확도", "실제 성능"), each = length(x_curve))
)

# 그래프 그리기
ggplot() +
  # 곡선
  geom_line(data = curve_data, 
           aes(x = complexity, y = accuracy, linetype = dataset, color = dataset),
           size = 1) +
  # 모델 유형
  geom_point(data = model_types, 
            aes(x = complexity, y = accuracy),
            size = 4, color = "#3498db") +
  # 모델 레이블
  geom_text_repel(data = model_types,
                 aes(x = complexity, y = accuracy, label = type),
                 box.padding = 0.5, point.padding = 0.5,
                 force = 2, seed = 42) +
  # 라벨과 제목
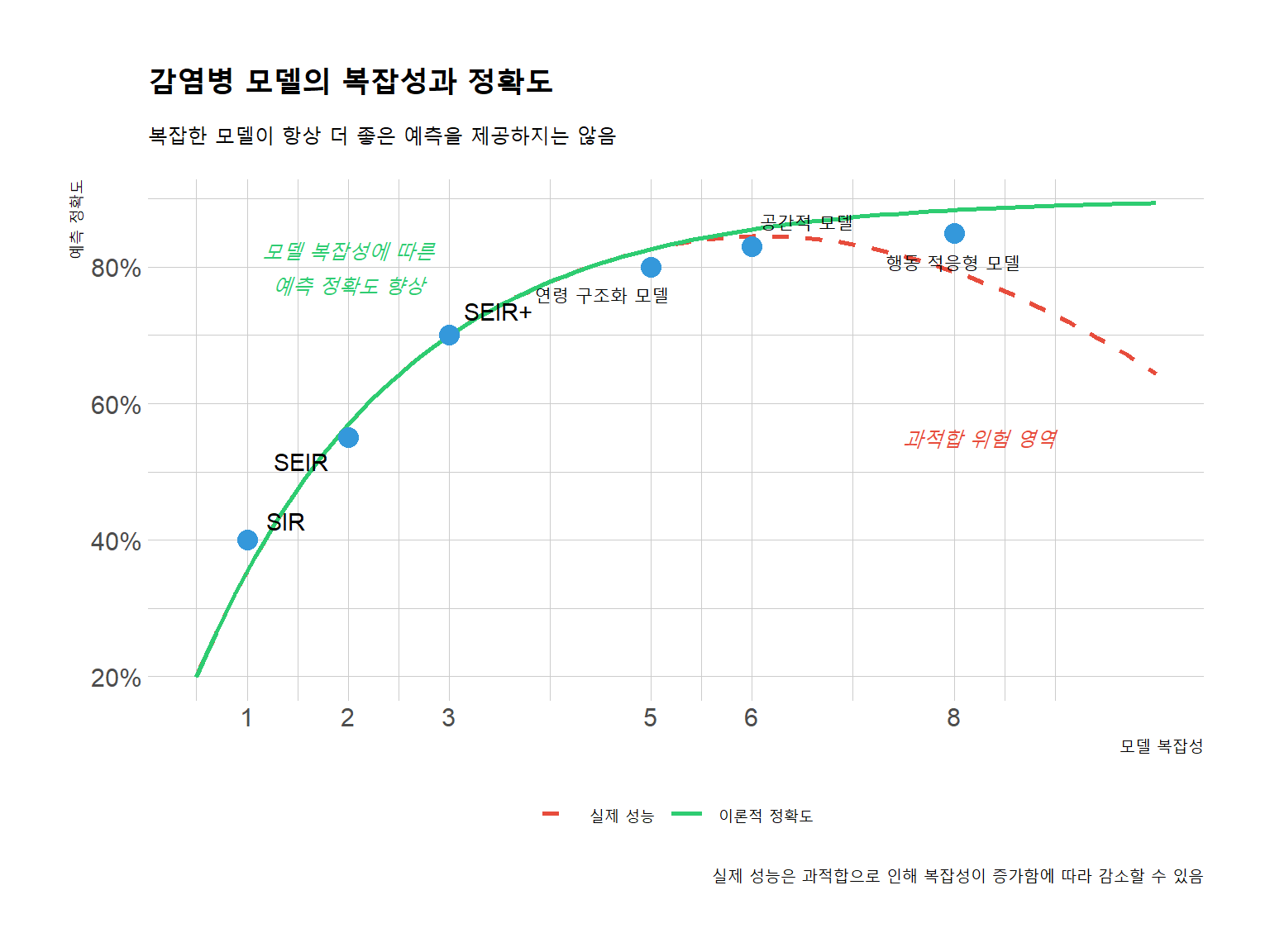
  labs(title = "감염병 모델의 복잡성과 정확도",
       subtitle = "복잡한 모델이 항상 더 좋은 예측을 제공하지는 않음",
       x = "모델 복잡성", 
       y = "예측 정확도",
       caption = "실제 성능은 과적합으로 인해 복잡성이 증가함에 따라 감소할 수 있음") +
  scale_color_manual(values = c("이론적 정확도" = "#2ecc71", "실제 성능" = "#e74c3c")) +
  scale_linetype_manual(values = c("이론적 정확도" = "solid", "실제 성능" = "dashed")) +
  scale_x_continuous(breaks = c(1, 2, 3, 5, 6, 8)) +
  scale_y_continuous(labels = scales::percent) +
  theme_ipsum_rc() +
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        plot.title = element_text(face = "bold", size = 16),
        plot.subtitle = element_text(size = 12),
        axis.title = element_text(size = 12)) +
  # 주석
  annotate("text", x = 7.5, y = 0.55, 
           label = "과적합 위험 영역", 
           color = "#e74c3c", fontface = "italic", hjust = 0) +
  annotate("text", x = 2, y = 0.8, 
           label = "모델 복잡성에 따른\n예측 정확도 향상", 
           color = "#2ecc71", fontface = "italic")

감염병 모델 개선 과정: 모델 복잡성과 정확도 사이의 관계

모델은 현실이 아니지만, 현실을 이해하는 도구다

통계학자 조지 박스(George Box)는 말했다. “모든 모델은 틀렸지만, 일부는 유용하다 (All models are wrong, but some are useful).”

감염병 모델도 마찬가지다. 완벽하지 않다. 그러나 복잡한 현실을 이해하는 데 도움을 준다. 가능한 미래를 탐색하게 해준다. 정책 결정에 정보를 제공한다.

중요한 것은 모델의 한계를 인정하는 것이다. 모델 결과를 절대적 진리로 받아들이면 안 된다. 하나의 참고 자료로 봐야 한다.

모델과 현실 사이의 간격은 항상 존재할 것이다. 그러나 그 간격을 좁히려는 노력은 계속되어야 한다. 다음 감염병이 찾아왔을 때, 우리는 더 준비되어 있을 수 있다.

그때 우리는 다시 물을 것이다. “이 모델은 현실을 얼마나 잘 반영하고 있는가?”